Number System in Hindi

Table of Contents

What is Number System | Number System in Hindi

इस आर्टिकल में हम संख्या प्रणाली ( number system in Hindi) को समझने का प्रयास करेंगे। सभी दशमलव संख्या प्रणाली(decimal number System) से भली भांति परिचित होंगे। decimal number system में किसी भी संख्या को प्रदर्शित करने के लिए 0 , 1, 2, 3, 4, 5, 6, 7, 8, तथा 9 अंक प्रयोग किये जाते हैं । इस प्रणाली का आधार(Base of radix) 10 है । रेडिक्स किसी प्रणाली में प्रयुक्त किये जाने वाले अंकों की संख्या है । कोई भी संख्या अंकों का एक समूह होती है । उदहारणत: 343.95 एक ऐसी संख्या है जिसमे पूर्णांक का मान 343 है तथा भिन्नात्मक भाग 0.95 है। पूर्णांक एवं भिन्नात्मक भाग एक रेडिक्स पॉइंट (.) द्वारा एक दुसरे से अलग रहते हैं । रेडिक्स पॉइंट डेसीमल पॉइंट भी कहलाता है । डेसीमल प्रणाली के अतिरिक्त कुछ अन्य संख्या प्रणाली भी हैं जो निम्न प्रकार हैं – Read this article in English

बाइनरी प्रणाली – binary number system
ऑक्टल संख्या प्रणाली -octal number system
हेक्साडेसीमल संख्या प्रणाली -Hexadecimal number system

डेसीमल Sankhya Paddhati | Decimal Number System in Hindi

डेसीमल संख्या प्रणाली हमारे दैनिक जीवन में व्यापक रूप से प्रयोग की जाती है। डेसीमल प्रणाली में लिखी गयी प्रत्येक संख्या के प्रत्येक अंक का अपना एक स्थायी मान होता है । इसे गुणक या Multiplying factor भी कहते हैं । गुणक हजार, सैंकड़ा , दहाई तथा इकाई इत्यादि होते हैं । इसी प्रकार 1 से कम मान की संखाओं को प्रदर्शित करने के लिए अंक दशमलव पॉइंट के के दाई तरफ लिखें जाते हैं तथा इसके स्थानीय मान क्रमशः 1_/10, 1_{/100 ,}1_/1000से गुणा करने पर प्राप्त किये जा सकते हैं। जैसे डेसीमल संख्या 4343.95 को निम्न प्रकार प्रदर्शित किया जा सकता है।

(4343.95)₁₀=4X10³+3X10²+4X10¹+3X10⁰+9X10^-1+5X10^-2

उपरोक्त उदहारण में 4 को उसके स्थानीय मान एक हजार(10³) से , 3 को सौ (10²) से , 4 को दस (10¹) से अवं 3 को एक (10⁰) से गुणा किया गया है। इसी प्रकार भिन्नात्मक भाग में 9 को 1_/10अर्थात 10^-1से एवं 5 को 1_/100अर्थात 10^-2से गुणा किया गया है।

सामान्यतया प्रत्येक संख्या प्रणाली में प्रतीकों(symbols) का एक सेट होता है जिन्हें अंक (डिजिट) कहते हैं । प्रत्येक प्रणाली में जोड़ने, घटाने , गुणा करने तथा भाग देने के नियम होते हैं। इन अंकों का समूह संख्या कहलाता है । संख्या के दो भाग होते हैं :(I) पूर्णांक(Integer) तथा (II) भिन्नात्मक (fractional) भाग । पूर्णांक तथा भिन्नात्मक भाग एक बिंदु (.) द्वारा अलग किये जाते हैं । इस बिंदु को रेडिक्स पॉइंट ( radix point) या दशमलव कहते हैं । उदहारणत: यदि एक संख्या में n पूर्णांक, m भिन्नात्मक अंक तथा रेडिक्स b है तब यह संख्या (N) निम्न प्रकार लिखी जा सकती हैं ।

जँहा N= एक संख्या
b=रेडिक्स अथवा प्रणाली की आधार संख्या
n= पूर्णांक भाग में अंकों की संख्या
m= भिन्नात्मक भाग में अंकों की संख्या
dn-1 = Most Significant digit(MSD)
d-m= Least significant digit(LSD)

विभिन्न Sankhya Paddhati के अभिलक्षण | Characteristics of various number systems

विभिन्न संख्या प्रणालियों के रेडिक्स तथा उनमे प्रयुक्त प्रतीक नीचे दिए गए हैं ।

Binary Number System in Hindi | बाइनरी संख्या प्रणाली

इस प्रणाली में केवल दो अंक 0 और 1 प्रयोग किये जाते हैं । अतः इस प्रणाली की आधार संख्या (रेडिक्स) 2 है । बाइनरी अंक 0 और 1 बिट्स कहलाते हैं । उदाहरणत : 10101 एक बाइनरी संख्या है क्युकी इसमें केवल 0 और 1 अंकों को ही प्रयोग किया गया है । इसी प्रकार 10101.1101 भी एक बाइनरी संख्या है संख्या में 10101 के पश्चात् प्रयुक्त बिंदु (.) बाइनरी बिंदु (binary point) कहलाता है । बाइनरी बिंदु के बायीं तथा दायीं ओर के स्थान के मान 2 की बढती हुई तथा घटती हुई घात (power ) में परिवर्तित होते हैं ।

बाइनरी संख्या का दशमलव मान निम्न प्रकार ज्ञात कर सकते हैं :

बाइनरी(101011)₂=1×2⁵+0x2⁴+1×2³+0x2²+1×2¹+1×2⁰

=32+08+8+0+2+1

=(43)₁₀दशमलव प्रणाली में

इसी प्रकार भिन्नात्मक बाइनरी संख्या को डेसीमल में परिवर्तित करने के लिए बाइनरी पॉइंट के दायीं ओर के अंकों को क्रमशः 2 ^-1, 2^-2, 2^-3 इत्यादि से गुणा किया जाता है ।

उदाहरणत: (0.10101)₂=1×2^-1+0x2^-2+1×2^-3+0x2^-4+1×2^-5

=1/2+0+1/8+0+1/32

=(0.65625)₁₀दशमलव प्रणाली में

Octal Number System in hindi | ऑक्टल संख्या प्रणाली

किसी भी संख्या प्रणाली का आधार( base or radix) उसमें प्रयुक्त अंकों की संख्या के बराबर होता है। ऑक्टल संख्या प्रणाली में 0 से 7 तक अंक डेसीमल प्रणाली की भांति होते हैं । ऑक्टल प्रणाली में अधिकतम अंक 7 है । इसमें 8 और 9 के अंक नही होते हैं ।अतः ऑक्टल प्रणाली में रेडिक्स का मान 8 है ।

बाइनरी को ऑक्टल प्रणाली में परिवर्तित करने के लिए 3-3 बिट्स के समूह बनाये जाते हैं तथा प्रत्येक समूह का मान डेसीमल में लिखने पर ऑक्टल संख्या प्राप्त होती है । उदाहरणत:

बाइनरी संख्या- 11111011110101

3-3 बिट्स के समूह 11, 111, 011, 110, 101

प्रत्येक समूह का मान डेसीमल में लिखने पर 3 7 3 6 5 _{(ऑक्टल)}

अतः (37365)₈बाइनरी संख्या (11111011110101)₂का ऑक्टल तुल्यांक है। ऑक्टल प्रणाली में 7 से अधिक मान की संख्याएँ लिखने के लिए दो डेसीमल डिजिट एक साथ प्रयुक्त किये जाते हैं । उदाहरणत: ऑक्टल में 10, डेसीमल प्रणाली के 8 को प्रदर्शित करता है ।

Hexadecimal Number system in hindi | हेक्साडेसीमल संख्या प्रणाली

माइक्रोप्रोसेसर के कार्यों में हेक्साडेसीमल प्रणाली का व्यापक उपयोग किया जाता है। हेक्साडेसीमल प्रणाली की आधार संख्या 16 है । इस प्रणाली में 0 से 9 तक अंक डेसीमल प्रणाली की भांति ही होते हैं । हेक्साडेसीमल प्रणाली में 10 को A द्वारा, 11 को B द्वारा, 12 को C द्वारा, 13 को D द्वारा, 14 को E द्वारा, 15 को F द्वारा तथा डेसीमल संख्या 16 को हेक्साडेसीमल प्रणाली में 10 द्वारा प्रदर्शित किया जाता है। डेसीमल संख्या 17 को 11 द्वारा, 18 को 12 द्वारा और 32 को 20 द्वारा प्रदर्शित करते हैं । नीचे टेबल में कुछ डेसीमल संख्याओं के बाइनरी एवं हेक्साडेसीमल तुल्यांक प्रदर्शित किये गए हैं।

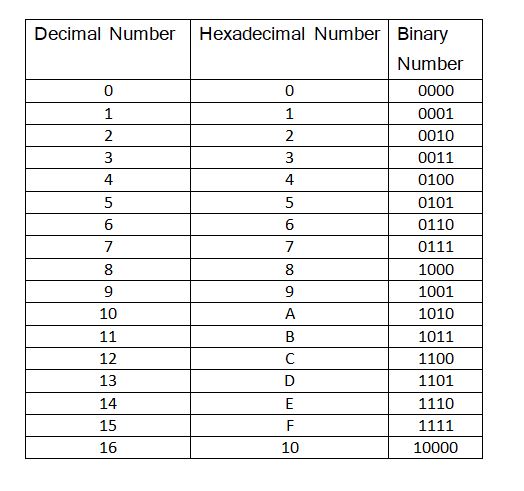
हेक्साडेसीमल प्रणाली में किसी संख्या के प्रत्येक अंक का स्थानीय मान 16 की किसी घात(power) द्वारा प्रदर्शित किया जाता है। हेक्साडेसीमल संख्या के अंकों के स्थानीय मान निम्न प्रकार होते हैं ।

16⁴ 16³ 16² 16¹ 16⁰ . 16^-1 16^-2 16^-3

इस प्रकार हेक्साडेसीमल संख्या को डेसीमल संख्या में परिवर्तित करने के लिए प्रत्येक डिजिट को उसके स्थानीय मान से गुणा कर, सभी गुणनफलों को जोड़ा जाता है । उदाहरणत: हेक्साडेसीमल संख्या 5A9 का डेसीमल तुल्यांक निम्न प्रकार ज्ञात किया जा सकता है-

(5A9)₁₆= 5×16²+Ax16¹+9×16⁰

=1280+10×16+9

=(1449)₁₀(डेसीमल संख्या )

आशा करते हैं की संख्या प्रणाली (number system in hindi) पर ये आर्टिकल आपको पसंद आया होगा। किसी भी प्रकार के सुझाव या फीडबैक के लिए आप कमेंट बॉक्स में आमंत्रित हैं।

और भी पढ़ें